En 1966, el matemático austríaco Leo Moser planteó la siguiente pregunta:
Si un pasillo tiene 1 metro de ancho, ¿cuál es el tamaño del mayor sofá que puede girar en una esquina de esta galería?
El problema no ha sido aún resuelto…
Este problema es una idealización en dimensión dos de un asunto de la vida real. De manera más precisa, la cuestión se puede enunciar del siguiente modo:
Tenemos un objeto rígido -un sofá- de dimensión 2 que debe maniobrarse a través de una región plana en forma de L. Las patas del sofá miden 1 unidad -como el pasillo- y se trata de encontrar el área A del mayor objeto que sea capaz de realizar este movimiento.
A es la constante del sofá y su valor exacto aún no se conoce.
Como un semicírculo de radio unidad puede doblar la esquina, una cota inferior para la constante del sofá es de π/2 (aproximadamente 1,570796327…)
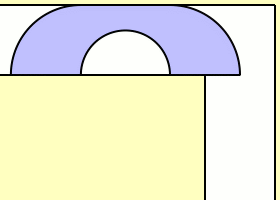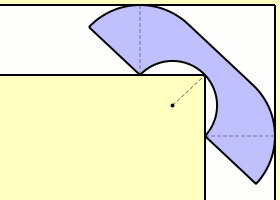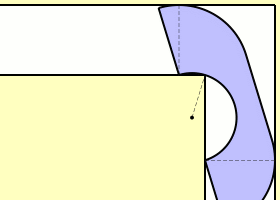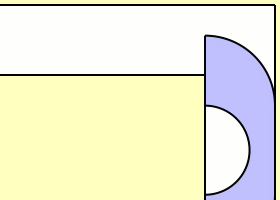
En 1968, el británico John Michael Hammersley mostró que un sofá de una forma similar a un auricular telefónico -ver la imagen de arriba- podría girar en la zona del pasillo en forma de L aunque su área fuera mayor que 2m2. De hecho probó que en ese caso A está acotado inferiormente por π/2 + 2/π (aproximadamente 2,207416099…).
En 1992, Joseph Gerver [Joseph L. Gerver, On moving a sofa around a corner, Geometriae Dedicata, Vol. 42, No. 3 (1992), 267-283, DOI: 10.1007/BF02414066] mejoró un poco más esta cota inferior (aproximadamente 2,219531669…).
En el otro sentido, Neal R. Wagner prueba en 1976 [Neal R. Wagner, The Sofa Problem, The American Mathematical Monthly,Vol. 83, No. 3 (Mar., 1976), 188-189, pdf] que A debe ser menor o igual que la raíz cuadrada de 8 (aproximadamente 2,8284…).
Pero el problema continúa abierto… ¿cuál es el valor exacto de A?
Visto en Futility Closet









Veo que Gerver es el mismo que demostró que la función de Riemann sí es diferenciable en algunos puntos: http://1.usa.gov/OlwO2W
Me gustaMe gusta
Reblogueó esto en Martams's Blogy comentado:
#HaceCuatroAños El problema del sofá
Me gustaMe gusta